Advertisements
Advertisements
प्रश्न
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
उत्तर
Let two similar triangles be ΔABC and ΔPQR.
So, ΔABC ∼ ΔPQR
By area theorem of similar triangles,
`(ar(ΔABC))/(ar(ΔPQR)) = ((BC)/(QR))^2` ......(i)
According to question,
ar(ΔABC) = ar(ΔPQR)
Substituting the values in equation (i),
`(ar(ΔABC))/(ar(ΔABC)) = ((BC)/(QR))^2`
⇒ 1 = `((BC)/(QR))^2`
⇒ (QR)2 = (BC)2
⇒ BC = QR
Similarly, AB = PQ and AC = PR.
Since sides of one triangle are equal to corresponding sides of another triangle
So, by SSS rule of congruence,
ΔABC ≅ ΔPQR
Hence proved.
APPEARS IN
संबंधित प्रश्न
If ∆ABC is similar to ∆DEF such that ∆DEF = 64 cm2 , DE = 5.1 cm and area of ∆ABC = 9 cm2 . Determine the area of AB
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half the area of the similar Triangle ACF described on the diagonal AC as base
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
D and E are points on the sides AB and AC respectively of a ∆ABC such that DE || BC and divides ∆ABC into two parts, equal in area. Find
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
In Figure, DE || BC If DE = 4 cm, BC = 6 cm and Area (ΔADE) = 16 cm2, find the area of ΔABC.
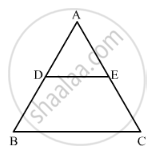
In Figure, DE || BC If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25 cm2, find the area of ΔABC.
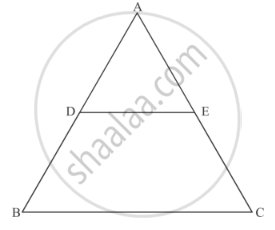
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
In the given figure DE || AC which of the following is true?
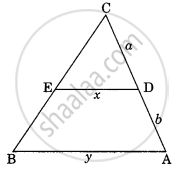
Find the length of ST, if ΔPQR ∼ ΔPST.

