Advertisements
Advertisements
प्रश्न
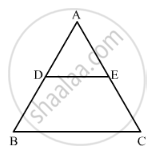
In Figure, DE || BC If DE = 4 cm, BC = 6 cm and Area (ΔADE) = 16 cm2, find the area of ΔABC.
उत्तर
We have, DE || BC, DE = 4 cm, BC = 6 cm and area (Δ𝐴𝐷𝐸) = 16 cm2
In ΔADE and ΔABC
∠A = ∠A [Common]
∠ADE = ∠ABC [Corresponding angles]
Then, ΔADE ~ ΔABC [By AA similarity]
∴ By area of similar triangle theorem
`("Area"(triangleADE))/("Area"(triangleABC))="DE"^2/"BC"^2`
`rArr16/("Area"(triangleABC))=4^2/6^2`
⇒ Area (ΔABC) = `(16xx36)/16=36"cm"^2`
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
If the areas of two similar triangles are equal, prove that they are congruent.
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
If ΔABC ~ ΔDEF such that AB = 5 cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
ΔABC ~ ΔPQR. In ΔABC, AB = 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB:PQ = 3:2, then construct ΔABC and ΔPQR.
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
