Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
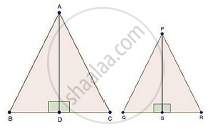
उत्तर
We have,
ΔABC ~ ΔPQR
Area (ΔABC) = 81 cm2,
Area (ΔPQR) = 49 cm2
And AD and PS are the altitudes
By area of similar triangle theorem
`("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2`
`rArr81/49="AB"^2/"PQ"^2`
`rArr9/7="AB"/"PQ"` ….(i) [Taking square root]
𝐼𝑛 ΔABD and ΔPQS
∠B = ∠Q [ΔABC ~ ΔPQR]
∠ ADB = ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PQ"="AD"/"PS"` …(ii) [Corresponding parts of similar Δ are proportional]
Compare (1) and (2)
`"AD"/"PS"=9/7`
∴ Ratio of altitudes = 9/7
Since, the ratio of the area of two similar triangles is equal to the ratio of the squares of the squares of their corresponding altitudes and is also equal to the squares of their corresponding medians.
Hence, ratio of altitudes = Ratio of medians = 9 : 7
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
In Figure, DE || BC If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25 cm2, find the area of ΔABC.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
