Advertisements
Advertisements
प्रश्न
In Figure, DE || BC If DE = 4 cm, BC = 6 cm and Area (ΔADE) = 16 cm2, find the area of ΔABC.
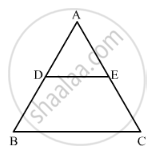
उत्तर
We have, DE || BC, DE = 4 cm, BC = 6 cm and area (Δ𝐴𝐷𝐸) = 16 cm2
In ΔADE and ΔABC
∠A = ∠A [Common]
∠ADE = ∠ABC [Corresponding angles]
Then, ΔADE ~ ΔABC [By AA similarity]
∴ By area of similar triangle theorem
`("Area"(triangleADE))/("Area"(triangleABC))="DE"^2/"BC"^2`
`rArr16/("Area"(triangleABC))=4^2/6^2`
⇒ Area (ΔABC) = `(16xx36)/16=36"cm"^2`
APPEARS IN
संबंधित प्रश्न
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (ΔADE): Area (ΔABC) = 3: 4
If ΔABC is similar to ΔDEF such that 2 AB = DE and BC = 8 cm then EF is equal to ______.
In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = ______.
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
Find the length of ST, if ΔPQR ∼ ΔPST.

If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
