Advertisements
Advertisements
प्रश्न
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
उत्तर
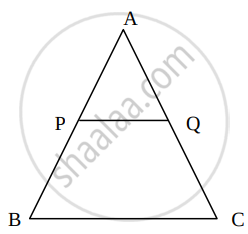
We have,
PQ || BC
And ar(ΔAPQ) = ar(trap. PQCB)
⇒ ar(ΔAPQ) = ar(ΔABC) – ar(ΔAPQ)
⇒ 2ar(ΔAPQ) = ar(ΔABC) ...(i)
In ΔAPQ and ΔABC
A = ∠A ...[Common]
∠APQ = ∠B ...[Corresponding angles]
Then, ΔAPQ ~ ΔABC ...[By AA similarity]
∴ By area of similar triangle theorem
`("Area"(triangleAPQ))/("Area"(triangleABC)) = "AP"^2/"AB"^2`
`rArr("Area"(triangleAPQ))/(2"Area"(triangleAPQ)) ="AP"^2/"AB"^2` ...[By using (i)]
`rArr1/2 = "AP"^2/"AB"^2`
`rArr1/sqrt2 = "AP"/"AB"^2`
`rArr1/sqrt2 = "AP"/"AB"` ...[Taking square root]
`rArr1/sqrt2 = (AB - BP)/(AB)`
`rArr1/sqrt2 = "AB"/"AB"-"BP"/"AB"`
`rArr1/sqrt2 = 1 - "BP"/"AB"`
`rArr"BP"/"AB" = 1 - 1/sqrt2`
`rArr"BP"/"AB" = (sqrt2-1)/sqrt2`
APPEARS IN
संबंधित प्रश्न
In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD and AB = 2 × CD. If the area of ∆AOB = 84 cm2 . Find the area of ∆COD
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.