Advertisements
Advertisements
प्रश्न
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
पर्याय
3 : 4
3 : 5
5 : 3
25 : 81
उत्तर
3: 5
Let ΔABC and ΔPQR be two similar triangles.
According to the given condition,
`"A(ΔABC)"/"A(ΔPQR)" = 9/25` ...(Given)
But `"A(ΔABC)"/"A(ΔPQR)" = "AB"^2/"PQ"^2` ...(By the theorem of areas of similar triangles)
∴ `"AB"^2/"PQ"^2 = 9/25`
∴ `"AB"/"PQ" = 3/5`
∴ 3: 5 is the ratio of their corresponding sides.
APPEARS IN
संबंधित प्रश्न
If ∆ABC is similar to ∆DEF such that ∆DEF = 64 cm2 , DE = 5.1 cm and area of ∆ABC = 9 cm2 . Determine the area of AB
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD and AB = 2 × CD. If the area of ∆AOB = 84 cm2 . Find the area of ∆COD
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
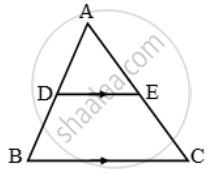
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
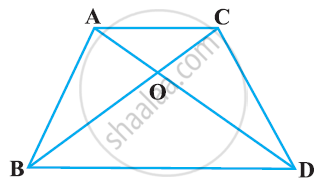
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
If ΔABC ~ ΔDEF such that AB = 5 cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
In the given figure DE || AC which of the following is true?