Advertisements
Advertisements
प्रश्न
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
उत्तर
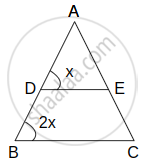
∴ Given: In `triangleABC`, DE || side BC.
`2A(triangleADE) = A(triangleDBCE)`
To find: `(AB)/(AD)`
To prove: BC = `sqrt3DE`
Proof: In `triangle ABC`
DE | | BC
∴ ∠ADE = ∠ ABC ...Corresponding angle ... (i)
∴ In `triangleADE` and `triangleABC` ∠BAC = ∠DAE ...Common angle
∠ADE = ∠ABC ...By (i)
∴ By A - A test
`triangleADE ≅ triangleABC`
`(AB)/(AD) = (BC)/(DE) = (AC)/(AE)`
Also, `2A(triangleADE) = A(DBCE)`
as `A(triangleABC) = A(triangleADE) +2(DBCE)`
`A(triangleABC) = A(triangleADE) + 2A(triangleADE)`
`A(triangleABC) = 3A(triangleADE)`
`(A(triangleABC))/(A(triangleADE) )= 3/1` ...(2)
`(A(triangleABC))/(A(triangleADE) )= (BC^2)/(DE^2)`
`3/1 = (BC^2)/(DE^2)` ...(Theorem of Area of similar triangle)
`3DE^2 = BC^2`
`sqrt3DE = BC` ...(By taking square root on both sides)
`BC = sqrt3 DE` Hence proved
APPEARS IN
संबंधित प्रश्न
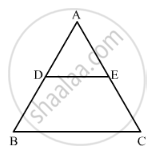
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
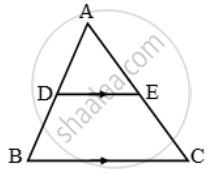
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
In Figure, DE || BC If DE = 4 cm, BC = 6 cm and Area (ΔADE) = 16 cm2, find the area of ΔABC.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
If D is a point on the side AB of ΔABC such that AD : DB = 3.2 and E is a Point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
ΔABC ~ ΔPQR. In ΔABC, AB = 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB:PQ = 3:2, then construct ΔABC and ΔPQR.
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
