SSC (English Medium)
SSC (Marathi Semi-English)
Academic Year: 2022-2023
Date & Time: 15th March 2023, 11:00 am
Duration: 2h
Advertisements
General Instructions :
- All questions are compulsory.
- Use of a calculator is not allowed.
- The numbers to the right of the questions indicate full marks.
- In case of MCQs (Q. No. 1(A)) only the first attempt will be evaluated and will be given credit.
- For every MCQ, the correct alternative (A), (B), (C) or (D) with a sub-question number is to be written as an answer.
- Draw proper figures for answers wherever necessary.
- The marks of construction should be clear. Do not erase them.
- Diagram is essential for writing the proof of the theorem.
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
Obtuse angled triangle
Acute angled triangle
Right-angled triangle
Equilateral triangle
Chapter: [0.02] Pythagoras Theorem
Chords AB and CD of a circle intersect inside the circle at point E. If AE = 4, EB = 10, CE = 8, then find ED.
7
5
8
9
Chapter: [0.03] Circle
Co-ordinates of origin are ______.
(0, 0)
(0, 1)
(1, 0)
(1, 1)
Chapter: [0.05] Co-ordinate Geometry
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
23 cm
26 cm
31 cm
25 cm
Chapter: [0.07] Mensuration
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
Chapter: [0.01] Similarity
In ∆RST, ∠S = 90°, ∠T = 30°, RT = 12 cm, then find RS.
Chapter: [0.02] Pythagoras Theorem
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
Chapter: [0.03] Circle
Find the distance between the points O(0, 0) and P(3, 4).
Chapter: [0.05] Co-ordinate Geometry
Advertisements
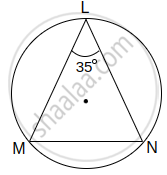
In the above figure, ∠L = 35°, find :
- m(arc MN)
- m(arc MLN)
Solution :
- ∠L = `1/2` m(arc MN) ............(By inscribed angle theorem)
∴ `square = 1/2` m(arc MN)
∴ 2 × 35 = m(arc MN)
∴ m(arc MN) = `square` - m(arc MLN) = `square` – m(arc MN) ...........[Definition of measure of arc]
= 360° – 70°
∴ m(arc MLN) = `square`
Chapter: [0.03] Circle
Show that, cotθ + tanθ = cosecθ × secθ
Solution :
L.H.S. = cotθ + tanθ
= `cosθ/sinθ + sinθ/cosθ`
= `(square + square)/(sinθ xx cosθ)`
= `1/(sinθ xx cosθ)` ............... `square`
= `1/sinθ xx 1/square`
= cosecθ × secθ
L.H.S. = R.H.S
∴ cotθ + tanθ = cosecθ × secθ
Chapter: [0.06] Trigonometry
Find the surface area of a sphere of radius 7 cm.
Solution :
The surface area of the sphere = 4πr2
= `4 xx 22/7 xx square^2`
= `4 xx 22/7 xx square`
= `square xx 7`
∴ The surface area of the sphere = `square` sq.cm.
Chapter: [0.07] Mensuration
In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, Find BQ.

Chapter: [0.01] Similarity
Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
Chapter: [0.02] Pythagoras Theorem
In the given figure, points G, D, E, and F are concyclic points of a circle with centre C. ∠ECF = 70°, m(arc DGF) = 200°. Find m(arc DE) and m(arc DEF).
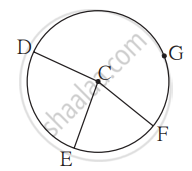
Chapter: [0.03] Circle
Show that points A(–1, –1), B(0, 1), C(1, 3) are collinear.
Chapter: [0.05] Co-ordinate Geometry
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
Chapter: [0.06] Trigonometry
Advertisements
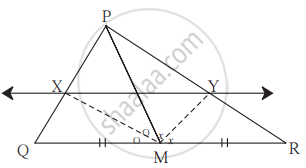
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.
Complete the proof by filling in the boxes.
solution:
In ∆PMQ,
Ray MX is the bisector of ∠PMQ.
∴ `("MP")/("MQ") = square/square` .............(I) [Theorem of angle bisector]
Similarly, in ∆PMR, Ray MY is the bisector of ∠PMR.
∴ `("MP")/("MR") = square/square` .............(II) [Theorem of angle bisector]
But `("MP")/("MQ") = ("MP")/("MR")` .............(III) [As M is the midpoint of QR.]
Hence MQ = MR
∴ `("PX")/square = square/("YR")` .............[From (I), (II) and (III)]
∴ XY || QR .............[Converse of basic proportionality theorem]
Chapter: [0.01] Similarity
Find the coordinates of point P where P is the midpoint of a line segment AB with A(–4, 2) and B(6, 2).
Solution :

Suppose, (–4, 2) = (x1, y1) and (6, 2) = (x2, y2) and co-ordinates of P are (x, y).
∴ According to the midpoint theorem,
x = `(x_1 + x_2)/2 = (square + 6)/2 = square/2 = square`
y = `(y_1 + y_2)/2 = (2 + square)/2 = 4/2 = square`
∴ Co-ordinates of midpoint P are `square`.
Chapter: [0.05] Co-ordinate Geometry
In ∆ABC, seg AP is a median. If BC = 18, AB2 + AC2 = 260, Find AP.
Chapter: [0.02] Pythagoras Theorem
Prove the following theorem:
Angles inscribed in the same arc are congruent.
Chapter: [0.03] Circle
Draw a circle with a radius of 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Chapter: [0.04] Geometric Constructions
The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
Chapter: [0.07] Mensuration
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
Chapter: [0.01] Similarity
ΔSHR ~ ΔSVU. In ΔSHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and `"SH"/("SV")=3/5`. Construct ΔSVU.
Chapter: [0.04] Geometric Constructions
An ice cream pot has a right circular cylindrical shape. The radius of the base is 12 cm and the height is 7 cm. This pot is completely filled with ice cream. The entire ice cream is given to the students in the form of right circular ice cream cones, having a diameter of 4 cm and a height is 3.5 cm. If each student is given one cone, how many students can be served?
Chapter: [0.07] Mensuration

A circle touches side BC at point P of the ΔABC, from outside of the triangle. Further extended lines AC and AB are tangents to the circle at N and M respectively. Prove that : AM = `1/2` (Perimeter of ΔABC)
Chapter: [0.03] Circle
Eliminate θ if x = r cosθ and y = r sinθ.
Chapter: [0.06] Trigonometry
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam Geometry Mathematics 2 with solutions 2022 - 2023
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam Geometry Maths 2-2023 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Geometry Mathematics 2, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam.
How Maharashtra State Board 10th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Geometry Mathematics 2 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
