Advertisements
Advertisements
प्रश्न
In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, Find BQ.

उत्तर १

side AB || side PQ || side DC ...(Given)
∴ By the Property of three parallel lines and their transversals,
`"AP"/" PD" = "BQ"/"QC"`
∴ `15/12 = "BQ"/14`
∴ 15 × 14 = 12 × BQ
∴ BQ = `(15 × 14)/12`
∴ BQ = `(5 × 7)/2`
∴ BQ = `35/2`
∴ BQ = 17.5 units
उत्तर २
Construction: Join BD intersecting PQ at X.
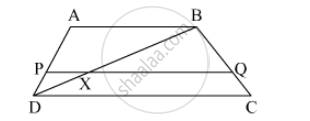
In △ ABD, PX || AB
`"PD"/"AP" = "XD"/"XB"` ....(By Basic proportionality theorem)(1)
In △BDC, XQ || DC
`"XD"/"XB" = "QC"/"BQ"` ....(By Basic proportionality theorem)(2)
From (1) and (2), we get
∴ `"PD"/"AP" = "QC"/"BQ"`
∴ `12/15 = 14/"BQ"`
∴ 12 × BQ = 15 × 14
∴ BQ = `(15 × 14)/12`
∴ BQ = `(5 × 7)/2`
∴ BQ = `35/2`
∴ BQ = 17.5 units
संबंधित प्रश्न
In ∆PQR, PM = 15, PQ = 25 PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.

In the given figure, seg PA, seg QB, seg RC, and seg SD are perpendicular to line AD.
AB = 60, BC = 70, CD = 80, PS = 280 then find PQ, QR, and RS.
In the given fig, XY || seg AC. If 2AX = 3BX and XY = 9. Complete the activity to Find the value of AC.
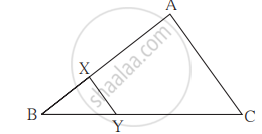
Activity: 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX" +"BX")/"BX" = (square + square)/square` ...(by componendo)
`"AB"/"BX" = square/square` ...(I)
ΔBCA ~ ΔBYX ...`square` test of similarity,
∴ `"BA"/"BX" = "AC"/"XY"` ...(corresponding sides of similar triangles)
∴ `square/square = "AC"/9`
∴ AC = `square` ...[From(I)]
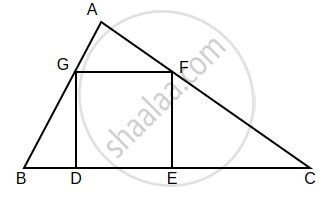
In the given figure, the vertices of square DEFG are on the sides of ∆ABC. ∠A = 90°. Then prove that DE2 = BD × EC. (Hint: Show that ∆GBD is similar to ∆CFE. Use GD = FE = DE.)

In the above figure, line l || line m and line n is a transversal. Using the given information find the value of x.

In the above figure, line AB || line CD || line EF, line l, and line m are its transversals. If AC = 6, CE = 9. BD = 8, then complete the following activity to find DF.
Activity :
`"AC"/"" = ""/"DF"` (Property of three parallel lines and their transversal)
∴ `6/9 = ""/"DF"`
∴ `"DF" = "___"`
