Advertisements
Advertisements
प्रश्न
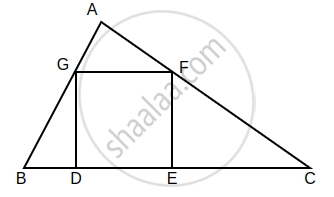
In the given figure, the vertices of square DEFG are on the sides of ∆ABC. ∠A = 90°. Then prove that DE2 = BD × EC. (Hint: Show that ∆GBD is similar to ∆CFE. Use GD = FE = DE.)
उत्तर १
Given: `square`DEFG is a square.
To prove: DE2 = BD × EC
Proof: DEFG is a square
In ΔGBD and ΔAGF,
∠GDB = ∠FAG = 90° ...(Each measures 90°)
∠AGF = ∠DBG ...(Common angle)
ΔGBD ∼ ΔAGF ...(AA Similarity Test) (1)
In ΔCFE and ΔAGF,

∠FAG = ∠CEF = 90° ...(Each measures 90°)
∠AFG = ∠ECF ...(Common angle)
ΔCFE ∼ ΔAGF ...(AA Similarity Test) (2)
From (1) and (2), we get
ΔCFE ∼ ΔGBD
∴ `"CE"/"GD" = "FE"/"BD"` ...(Corresponding sides of similar triangles are in proportional)
∴ `"CE"/"DE" = "DE"/"BD"` ...(∵ GD = FE = DE)
∴ DE2 = BD × CE
Hence proved.
उत्तर २
Given: `square`DEFG is a square.
To prove: DE2 = BD × EC
Proof: `square`DEFG is a square. ...(Given)
∴ DE = EF = GF = GD ...(Sides of a square) (I)
∠GDE = ∠DEF = 90° ...(Angles of a square)
∴ seg GD ⊥ sides BC and seg EF⊥ side BC.
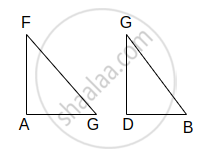
In ΔBAC and ΔBDG,
∠BAC ≅ ∠BDG ...(Each measures 90°)
∠ABC ≅ ∠DBG ...(Common angles)
∴ ΔBAC ~ ΔBDG ...(AA test of similarity) (II)
Similarly,
ΔBAC ~ ΔFEC ...(III)
∴ ΔBDG ~ ΔFEC ...[From II and III]
∴ `"BD"/"EF" = "GD"/"EC"` ...(Corresponding sides of similar triangles are in proportion)
∴ `"BD"/"DE" = "DE"/"EC"` ...(From 1)
∴ DE2 = BD × EC
संबंधित प्रश्न
In ∆PQR, PM = 15, PQ = 25 PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.

In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, Find BQ.

In the given figure, seg PA, seg QB, seg RC, and seg SD are perpendicular to line AD.
AB = 60, BC = 70, CD = 80, PS = 280 then find PQ, QR, and RS.
In the given fig, XY || seg AC. If 2AX = 3BX and XY = 9. Complete the activity to Find the value of AC.
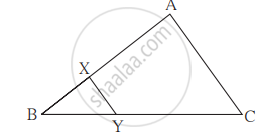
Activity: 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX" +"BX")/"BX" = (square + square)/square` ...(by componendo)
`"AB"/"BX" = square/square` ...(I)
ΔBCA ~ ΔBYX ...`square` test of similarity,
∴ `"BA"/"BX" = "AC"/"XY"` ...(corresponding sides of similar triangles)
∴ `square/square = "AC"/9`
∴ AC = `square` ...[From(I)]

In the above figure, line l || line m and line n is a transversal. Using the given information find the value of x.

In the above figure, line AB || line CD || line EF, line l, and line m are its transversals. If AC = 6, CE = 9. BD = 8, then complete the following activity to find DF.
Activity :
`"AC"/"" = ""/"DF"` (Property of three parallel lines and their transversal)
∴ `6/9 = ""/"DF"`
∴ `"DF" = "___"`
