Advertisements
Advertisements
प्रश्न
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
विकल्प
2 : 1
1 : 2
4 : 1
1 : 4
उत्तर
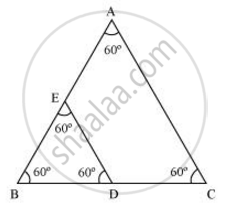
We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other. Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.
Let side of ΔABC = x
Therefore, side of ΔBDE = `x/2`
`∴ (area(ΔABC))/(area(ΔBDE)) = (x/(x/2))^2 =4/1`
Hence, the correct answer is (C).
APPEARS IN
संबंधित प्रश्न
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
