Advertisements
Advertisements
प्रश्न
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
उत्तर
We have, Area (ΔABC) = 36 cm2
Area (Δ𝐷𝐸𝐹) = 64 cm2
DE = 6.2 cm
And, ΔABC ~ ΔDEF
By area of similar triangle theorem
`("Area"(triangleABC))/(Area(triangleDEF))="AB"^2/"DE"^2`
`rArr36/64="AB"^2/6.2^2` [By taking square root]
`rArr"AB"=(6xx6.2)/8=4.65` cm
APPEARS IN
संबंधित प्रश्न
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
In Figure, DE || BC If DE = 4 cm, BC = 6 cm and Area (ΔADE) = 16 cm2, find the area of ΔABC.
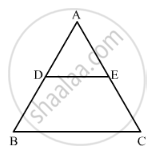
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
In the given figure DE || AC which of the following is true?
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.