Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
उत्तर
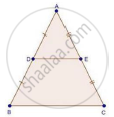
We have, D and E as the mid-points of AB and AC
So, according to the mid-point theorem
DE || BC and DE `=1/2`BC ...(i)
In ΔADE and ΔABC
∠A = ∠A [Common]
∠ADE = ∠B [Corresponding angles]
Then, ΔADE ~ ΔABC [By AA similarity]
By area of similar triangle theorem
`("Area"(triangleADE))/("Area"(triangleABC))="DE"^2/"BC"^2`
`=(1/2BC)^2/"BC"^2` [From (i)]
`=(1/4BC^2)/"BC"^2`
`=1/4`
APPEARS IN
संबंधित प्रश्न
If ∆ABC is similar to ∆DEF such that ∆DEF = 64 cm2 , DE = 5.1 cm and area of ∆ABC = 9 cm2 . Determine the area of AB
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
The ratio of corresponding sides of similar triangles is 3 : 5; then find the ratio of their areas.
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
