Advertisements
Advertisements
प्रश्न
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
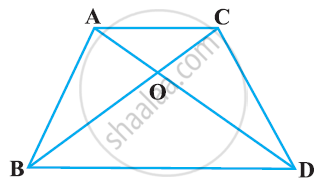
उत्तर
Let us draw two perpendiculars AP and DM on line BC.
We know that area of a triangle = `1/2 xx "Base" xx "Height"`
`:.(ar(triangleABC))/(ar(triangleDBC)) = (1/2 BC xx AP)/(1/2BC xx DM) = (AP)/(DM)`
In ΔAPO and ΔDMO,
∠APO = ∠DMO (Each = 90°)
∠AOP = ∠DOM (Vertically opposite angles)
∴ ΔAPO ∼ ΔDMO (By AA similarity criterion)
`:. (AP)/(DM) = (AO)/(DO)`
`=> (ar(triangleABC))/(ar(triangleDBC))=(AO)/(DO)`
APPEARS IN
संबंधित प्रश्न
In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD and AB = 2 × CD. If the area of ∆AOB = 84 cm2 . Find the area of ∆COD
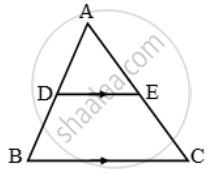
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
If ΔABC and ΔBDE are equilateral triangles, where D is the mid-point of BC, find the ratio of areas of ΔABC and ΔBDE.
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
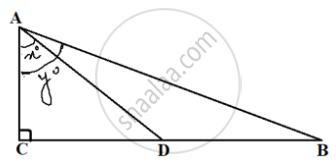
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
