Question

D and E are points on the sides AB and AC respectively of a ∆ABC such that DE || BC and divides ∆ABC into two parts, equal in area. Find

Answer 1

We have,

Area (∆ADE) = Area (trapezium BCED)

⇒ Area (∆ADE) + Area (∆ADE)

= Area (trapezium BCED) + Area (∆ADE)

⇒ 2 Area (∆ADE) = Area (∆ABC)

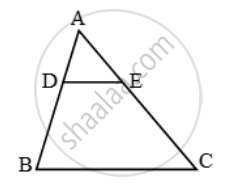
In ∆ADE and ∆ABC, we have

∠ADE = ∠B [∵ DE || BC ∴ ∠ADE = ∠B (Corresponding angles)] and, ∠A = ∠A [Common]

∴ ∆ADE ~ ∆ABC

`\Rightarrow \frac{Area\ (\Delta ADE)}{Area\ (\Delta ABC)}=(AD^2)/(AB^2)`

`(Area(DeltaADE))/(2Area(DeltaADE))=(AD^2)/(AB^2)`

`\Rightarrow \frac{1}{2}=( \frac{AD}{AB})^{2}\Rightarrow \frac{AD}{AB}=\frac{1}{\sqrt{2}}`

⇒ AB = √2 AD AB = √2 (AB – BD)

⇒ (√2 – 1) AB = √2 BD

`\Rightarrow \frac{BD}{AB}=\frac{\sqrt{2}-1}{\sqrt{2}}=\frac{2-\sqrt{2}}{2}`