Advertisements
Advertisements
प्रश्न
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (ΔADE): Area (ΔABC) = 3: 4
उत्तर
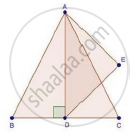
We have,
ΔABC is an equilateral triangle
Then, AB = BC = AC
Let, AB = BC = AC = 2x
Since, AD ⊥ BC then BD = DC = x
In ΔADB, by Pythagoras theorem
𝐴𝐵2 = (2𝑥)2 − (𝑥)2
⇒ 𝐴𝐷2 = 4𝑥2 − 𝑥2 = 3𝑥2
⇒ 𝐴𝐷 = `sqrt3`𝑥 cm
Since, ΔABC and ΔADE both are equilateral triangles then they are equiangular
∴ ΔABC ~ ΔADE [By AA similarity]
By area of similar triangle theorem
`("area"(triangleADE))/("area"(triangleABC))="AD"^2/"AB"^2`
`=(sqrt3x)^2/(2x)^2`
`=(3x^2)/(4x^2)`
`=3/4`
APPEARS IN
संबंधित प्रश्न
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
If the areas of two similar triangles are equal, prove that they are congruent.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
