Question

Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights

Answer 1

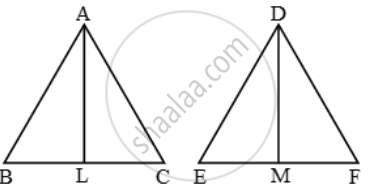
Let ∆ABC and ∆DEF be the given triangles such that AB = AC and DE = DF, ∠A = ∠D.

`and \frac{Area\ (\Delta ABC)}{Area\ (\Delta DEF)}=\frac{16}{25}  …….(i)`

Draw AL ⊥ BC and DM ⊥ EF.

Now, AB = AC, DE = DF

`\Rightarrow \frac{AB}{AC}=1\text{ and }\frac{DE}{DF}=1`

`\Rightarrow \frac{AB}{AC}=\frac{DE}{DF}\text{ }\Rightarrow \text{ }\frac{AB}{DE}=\frac{AC}{DF} `

Thus, in triangles ABC and DEF, we have

`\frac{AB}{DE}=\frac{AC}{DF}\text{ and } ∠A = ∠D [`

So, by SAS-similarity criterion, we have

∆ABC ~ ∆DEF

`\Rightarrow \frac{Area\ (\Delta ABC)}{Area\ (\DeltaDEF)}=(AL^2)/(DM^2)`

`\Rightarrow \frac{16}{25}=(AL^2)/(DM^2) `

`\frac{AL}{DM}=\frac{4}{5} `

AL : DM = 4 : 5