Advertisements
Advertisements
Question
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
Solution
It is given that ΔABC ~ ΔDEF
`:. (ar(triangleABC))/(ar(triangleDEF)) = ((AB)/(DE))^2 = ((BC)/(EF))^2=((AC)/(DF))^2`
Given that
EF = 15.4
ar(ΔABC) = 64 cm2
ar(ΔDEF) = 121 cm2
`:.(ar(ABC))/(ar(ΔDEF))=((BC)/(EF))^2`
`=>((64 cm^2)/(121 cm^2)) = (BC^2)/(15.4 cm)^2`
`=>(BC)/15.4 = (8/11)cm`
`=>BC = ((8xx15.4)/11)cm = (8 xx 1.4) cm = 11.2 cm`
APPEARS IN
RELATED QUESTIONS
If ∆ABC is similar to ∆DEF such that ∆DEF = 64 cm2 , DE = 5.1 cm and area of ∆ABC = 9 cm2 . Determine the area of AB
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
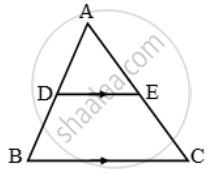
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
If ΔABC ~ ΔDEF such that AB = 5 cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
If D is a point on the side AB of ΔABC such that AD : DB = 3.2 and E is a Point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In the given figure DE || AC which of the following is true?
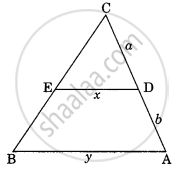
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
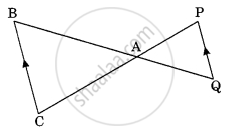
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
