Advertisements
Advertisements
Question
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Solution
To prove: In a right-angled triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides of the triangle.
Proof: Let PQR be a triangle, right-angled at P.
Draw PS ⊥ QR
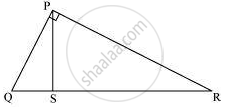
Now, we know that if a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, then the triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
∴ΔQSP ∼ ΔQPR
Therefore, `"QS"/"QP" = "QP"/"QR"` .....................(Since the sides of similar triangles are proportional)
⇒ QS. QR = Qp2 .......(1)
Also, we have
ΔPSR ∼ ΔQPR
Therefore, `"RS"/"RP" = "RP"/"RQ"`.............(Since the sides of similar triangles are proportional)
⇒ RS.RQ = RP2 … (2)
Adding equations (1) and (2), we obtain
QS.QR + RS.RQ = RP2 + QP2
⇒ QR. (QS + RS) = RP2 + QP2
⇒ QR.QR = RP2 + QP2
⇒ QR2 = RP2 + QP2
Thus, the square of the hypotenuse is equal to the sum of squares of the other two sides of the triangle.
APPEARS IN
RELATED QUESTIONS
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
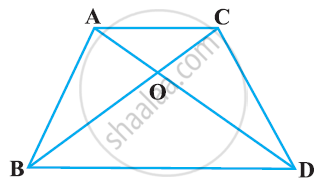
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
If D is a point on the side AB of ΔABC such that AD : DB = 3.2 and E is a Point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
