Advertisements
Advertisements
Question
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
Options
20.25 cm
27 cm
48 cm
64 cm
Solution
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is 27 cm.
Explanation:
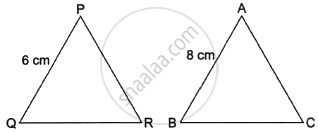
∵ Ratio of side = Ratio of perimeter
`\implies (PQ)/(AB) = ("Perimeter of" ΔPQR)/("Perimeter of" ΔABC)`
`\implies 6/8 = ("Perimeter of" ΔPQR)/36`
`\implies 3/4 = ("Perimeter of" ΔPQR)/36`
`\implies` Perimeter of ΔPQR = `(36 xx 3)/4`
= 9 × 3
= 27 cm
RELATED QUESTIONS
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
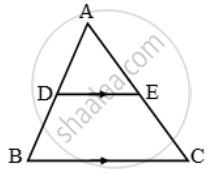
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
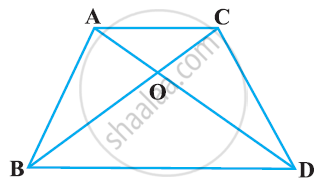
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
In the given figure DE || AC which of the following is true?
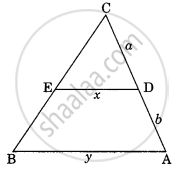
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
