Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram whose sides AB and BC are 18cm and 12cm respectively. G is a point on AC such that CG : GA = 3 : 5 BG is produced to meet CD at Q and AD produced at P. Prove that ΔCGB ∼ ΔAGP. Hence, fi AP.
उत्तर
In ΔCGB and ΔAGP
∠CGB = ∠AGP ...(vertically opposite angles)
∠GAP = ∠GCB ...(AD || BC, therefore alternate angles)
Therefore, ΔCGB ∼ ΔAGP ...(AA axiom)
∴ `"CG"/"GA" = "BC"/"AP"`
⇒ `(3)/(5) = (12)/"AP"`
⇒ AP = `(5 xx 12)/(3)`
⇒ AP = 20cm.
APPEARS IN
संबंधित प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
In the following figure, DE || OQ and DF || OR, show that EF || QR.

In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
From the figure, prove that ∆SUN ~ ∆RAY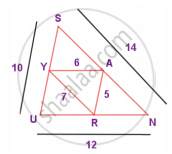
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
In ∠BAC = 90° and AD ⊥ BC. A then ______.

