Advertisements
Advertisements
प्रश्न
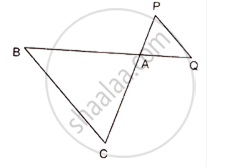
In figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm, find CA and AQ.
In the following figure, ΔACB ~ ΔAPQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ.
उत्तर
We have, ∆ACB ~ ∆APQ
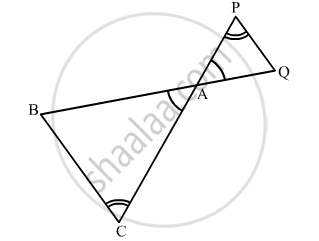
`\Rightarrow \frac{AC}{AP}=\frac{CB}{PQ}=\frac{AB}{AQ} `
`\Rightarrow \frac{AC}{AP}=\frac{CB}{PQ}\text{ and }\frac{CB}{PQ}=\frac{AB}{AQ}`
`\Rightarrow \frac{AC}{2.8}=\frac{8}{4}\text{ and }\frac{8}{4}=\frac{6.5}{AQ} `
`\Rightarrow \frac{AC}{2.8}=2\text{ and }\frac{6.5}{AQ}=2`
AC = (2 × 2.8) cm = 5.6 cm and `AQ=\frac{6.5}{2}cm=3.25cm`
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
See the given figure. DE || BC. Find EC.

In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
In ΔABC, DE is parallel to BC and DE = 3:8.
Find:
(i) AD : BD
(ii) AE, if AC = 16.
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
