Advertisements
Advertisements
प्रश्न
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

उत्तर
We have:
`(AB)/(DF)=3/6=1/2` and `(BC)/(DE)=4.5/9=1/2`
But , ∠ABC ≠ ∠EDF (Included angles are not equal)
Thus, this triangles are not similar.
APPEARS IN
संबंधित प्रश्न
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
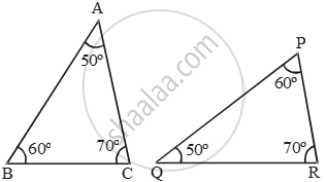
figure (i)
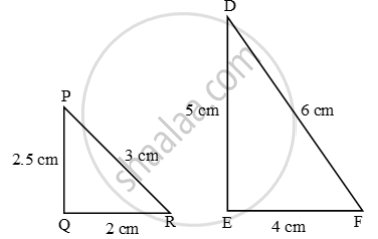
figure 2
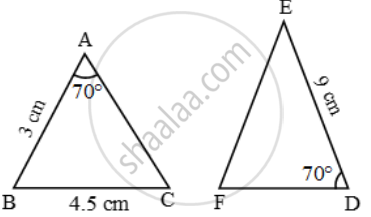
figure 3

figure 4
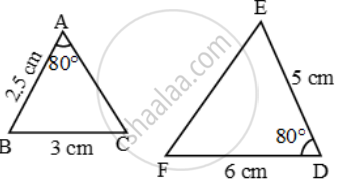
figure 5
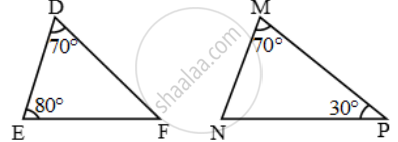
figure 6

figure 7
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

State, true or false:
Two congruent polygons are necessarily similar.
The two similar triangles are equal in area. Prove that the triangles are congruent.
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.

In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
Δ ABC ∼ Δ PQR such that AB= 1.5 cm and PQ=2. 1 cm. Find the ratio of areas of Δ ABC and ΔPQR.
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
A model of a ship is made to a scale 1 : 300.
- The length of the model of the ship is 2 m. Calculate the length of the ship.
- The area of the deck of the ship is 180,000 m2. Calculate the area of the deck of the model.
- The volume of the model is 6.5 m3. Calculate the volume of the ship.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
Given is a triangle with sides 3 cm, 5 cm and 6 cm. Find the sides of a triangle which is similar to the given triangle and its shortest side is 4.5 cm.
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
Find the scale factor in each of the following and state the type of size transformation:
Actual length = 12cm, Image length = 15cm.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
In a triangle ABC, AB = 4 cm, BC = 4.5 cm and CA = 5 cm. Construct ΔABC. Find the image A'B'C of the ΔABC obtained by enlarging it by a scale factor 2. Measure the sides of the image A'B'C' and show that AB:A'B' = AC:B'C' = CA:C'A'
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
Given ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 35° then ∠B = ?
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
