Advertisements
Advertisements
प्रश्न
In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

उत्तर
1) Area of a triangle = 1/2 x base x height
`:. A(triangle DEF) = 1/2 xx EF xx DH`
`:. 450 = 1/2 xx EF xx 18` ......(Substituting the given values)
`:. (450xx2)/18 = EF`
`:. EF = 50 :. EF = 50 cm`
2) `triangle DEF` and `triangle GEF` have then common base EF
∴ their areas are proportional to their corresponding heights
`:. (A(triangle DEF))/(A(triangle GEF)) = "DH"/"GK"`
`:. 450/(A(triangle GEF)) = 18/30` ....(Substituting the given values).
`:. A(triangle GEF) = (450xx30)/18 = 750 cm^2`
`:. A(triangle GEF) = 750 cm^2`
3) `A(squareDFGE) = A(squareDEF) + A(squareGEF)` ....(Area addition postulate)
= 450 + 750 = 1200cm2
`:. A(squareDFGE) = 1200 cm^2`
APPEARS IN
संबंधित प्रश्न
See the given figure. DE || BC. Find AD.

E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
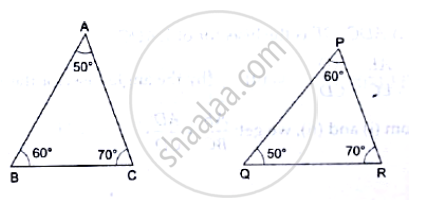
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
