Advertisements
Advertisements
प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
उत्तर
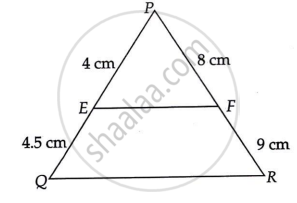
PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm
`("PE")/("EQ") = 4/4.5 = 40/45 = 8/9`
`("PF")/("FR") = 8/9`
`("PF")/("FR")=("PE")/("EQ")`
Therefore, EF is parallel to QR.
APPEARS IN
संबंधित प्रश्न
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.

Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
State, true or false:
Two congruent polygons are necessarily similar.
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.

In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
State the AA-similarity criterion
Are the triangles in the given figure similar? If yes, by which test?

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
ABCD and PQRS are similar figures. AB= 12cm, BC=x cm, CD= 15 cm, AD= 10 cm, PQ= 8 cm, QR = 5 cm, RS = m cm and PS = n cm .Find the values of x, m and n.
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `3/5` of the corresponding sides of the first triangle.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD : BD = 4 : 5 and EC = 2.5cm, find AE.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where P is any point on side AB. Prove that CQ x PQ = QA x QD.
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.
PQ is perpendicular to BA and BD is perpendicular to AP.PQ and BD intersect at R. Prove that ΔABD ∼ ΔAPQ and `"AB"/"AP" = "BD"/"PQ"`.
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that ΔPTQ - DRTS
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The ground area in km2 that is represented by 2cm2 on the map.
A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
Areas of two similar triangles are equal then prove that triangles are congruent
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is ______.

In the given figure, ΔABC ∼ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; them the value of x is ______.

In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

