Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
उत्तर
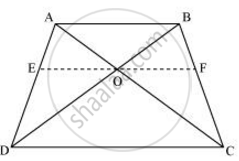
Draw a line EF through point O, such that EF || CD
In ΔADC, EO || CD
By using basic proportionality theorem, we obtain
`("AE")/("ED") = ("AO")/("OC")` ...(1)
In ΔABD, OE || AB
So, by using basic proportionality theorem, we obtain
`("ED")/("AE") = ("OD")/("BO")`
⇒ `("AE")/("ED") = ("BO")/("OD")` ...(2)
From equations (1) and (2), we obtain
⇒ `("AO")/("OC") = ("BO")/("OD")`
⇒ `("AO")/("BO") = ("OC")/("OD")`
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.
1) Prove ΔADB ~ ΔCDA.
2) If BD = 18 cm CD = 8 cm Find AD.
3) Find the ratio of the area of ΔADB is to an area of ΔCDA.

In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
In the given figure, ∠CAB = 90° and AD⊥BC. Show that ΔBDA ~ ΔBAC. If AC = 75cm, AB = 1m and BC = 1.25m, find AD.

The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

Are the triangles in the given figure similar? If yes, by which test?

If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
On a map drawn to a scale of 1 : 25000, a rectangular plot of land, ABCD is measured as AB= 12 cm and BC = 16cm. calculate the diagonal distance of the plot in km and the plot area in km2 .
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
In the figure, PR || SQ. If PR = 10cm, PT = 5cm, TQ = 6cm and ST = 9cm, calculate RT and SQ.
Given is a triangle with sides 3 cm, 5 cm and 6 cm. Find the sides of a triangle which is similar to the given triangle and its shortest side is 4.5 cm.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The length of a scale in km represented by 1cm on the map.
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
Check whether the triangles are similar and find the value of x
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
From the figure, prove that ∆SUN ~ ∆RAY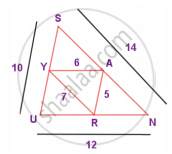
Given ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 35° then ∠B = ?
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
If ΔABC ~ ΔLMN and ∠B = 40°, then ∠M = ? Give reason.
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?

In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
