Advertisements
Advertisements
प्रश्न
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
उत्तर
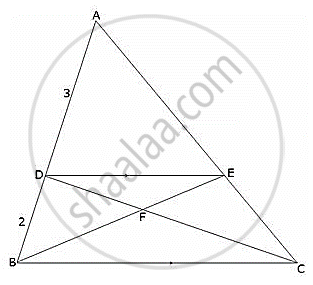
i. Given, DE || BC and `(AD)/(DB) = 3/2`
In ΔADE and ΔABC,
∠A = ∠A ...(Corresponding Angles)
∠ADE = ∠ABC ...(Corresponding Angles)
∴ ΔADE ∼ ΔABC ...(By AA- similarity)
`(AD)/(AB) = (AE)/(AC) = (DE)/(BC)` ...(1)
Now, `(AD)/(AB) = (AD)/(AD + DB) = 3/(3 + 2) = 3/5`
Using (1), we get `(AD)/(AE) = 3/5 = (DE)/(BC)` ...(2)
ii. In ∆DEF and ∆CBF,
∠FDE =∠FCB ...(Alternate Angle)
∠DFE = ∠BFC ...(Vertically Opposite Angle)
∴ ∆DEF ∼ ∆CBF ...(By AA- similarity)
`(EF)/(FB) = (DE)/(BC) = 3/5` Using (2)
`(EF)/(FB) = 3/5`
iii. Since the ratio of the areas of two similar triangles is equal to the square of the ratio of the corresponding sides, therefore.
`"Area of ΔDFE"/"Area of ΔCBF" = (EF^2)/(FB^2) = 3^2/5^2 = 9/25`
APPEARS IN
संबंधित प्रश्न
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
In the given figure, ∠CAB = 90° and AD⊥BC. Show that ΔBDA ~ ΔBAC. If AC = 75cm, AB = 1m and BC = 1.25m, find AD.

Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`

If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 5.6cm, AD = 1.4cm, AC = 7.2cm, and AE = 1.8cm
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
