Question

In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.

1. Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`. 
2. Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
3. What is the ratio of the areas of ∆DEF and ∆BFC?

Answer 1

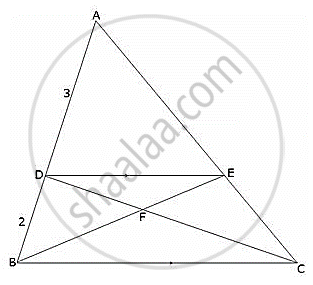
i. Given, DE || BC and `(AD)/(DB) = 3/2`

In ΔADE and ΔABC,

∠A = ∠A   ...(Corresponding Angles)

∠ADE = ∠ABC   ...(Corresponding Angles)

∴ ΔADE ∼ ΔABC   ...(By AA- similarity)

`(AD)/(AB) = (AE)/(AC) = (DE)/(BC)`   ...(1)

Now, `(AD)/(AB) = (AD)/(AD + DB) = 3/(3 + 2) = 3/5`

Using (1), we get `(AD)/(AE) = 3/5 = (DE)/(BC)`  ...(2)

ii. In ∆DEF and ∆CBF,

∠FDE =∠FCB   ...(Alternate Angle)

∠DFE = ∠BFC  ...(Vertically Opposite Angle)

∴ ∆DEF ∼ ∆CBF  ...(By AA- similarity)

`(EF)/(FB) = (DE)/(BC) = 3/5` Using (2)

`(EF)/(FB) = 3/5`

iii. Since the ratio of the areas of two similar triangles is equal to the square of the ratio of the corresponding sides, therefore.

`"Area of ΔDFE"/"Area of ΔCBF" = (EF^2)/(FB^2) = 3^2/5^2 = 9/25`