Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
उत्तर
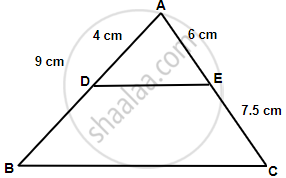
i. In ΔADE and ΔABC,
`(AE)/(EC) = 6/7.5 = 4/5`
`(AD)/(BD) = 4/5` ...(Since AB = 9 cm and AD = 4 cm)
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
ii. In ΔADE and ΔABC,
`(AE)/(EC) = 1.6/11 = 0.8/5.5`
`(AD)/(BD) = (0.8)/(6.3 - 8) = 0.8/5.5`
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
APPEARS IN
संबंधित प्रश्न
The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, find AB
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
State, true or false:
Two isosceles-right triangles are similar.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.

ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
PQ is perpendicular to BA and BD is perpendicular to AP.PQ and BD intersect at R. Prove that ΔABD ∼ ΔAPQ and `"AB"/"AP" = "BD"/"PQ"`.
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
