Advertisements
Advertisements
प्रश्न
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
उत्तर
In ΔABC, the coordinates of the vertices are A(–2, 0), B(2, 0), C(0, 2).
`AB = sqrt((2+2)^2 + (0 - 0)^2) = 4`
`BC = sqrt((0 - 2)^2 + (2 - 0)^2) =sqrt8 = 2sqrt2`
`CA = sqrt((0 + 2)^2 + (2 - 0)^2) = sqrt8 = 2sqrt2)`
In ΔPQR, the coordinates of the vertices are P(–4, 0), Q(4, 0), R(0, 4).
`PQ = sqrt((4+4)^2 + (0-0)^2) = 8`
`QR = sqrt((0 - 4)^2 + (4 - 0)^2) = 4sqrt2`
`PR= sqrt((0 + 4)^2 + (4 - 0)^2) = 4sqrt2`
Now, for ΔABC and ΔPQR to be similar, the corresponding sides should be proportional
So, `(AB)/(PQ) = (BC)/(QR) = (CA)/(PR)`
`=> 4/8 = (2sqrt2)/(4sqrt2) = (2sqrt2)/(4sqrt2) = 1/2`
Thus, ΔABC is similar to ΔPQR
APPEARS IN
संबंधित प्रश्न
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
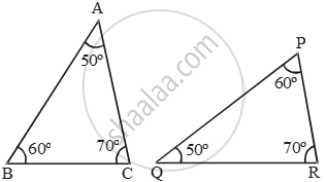
figure (i)
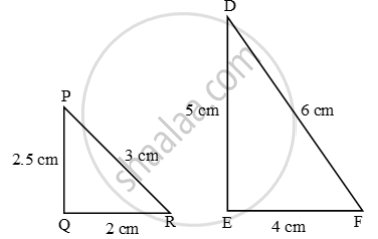
figure 2
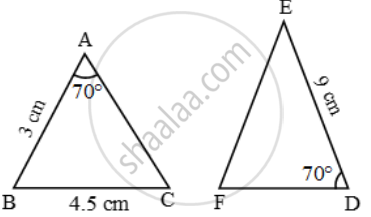
figure 3

figure 4
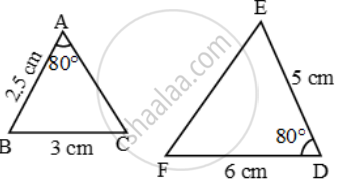
figure 5
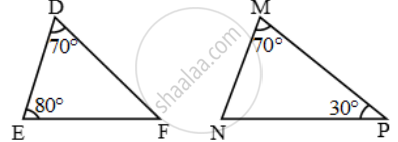
figure 6

figure 7
The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, find AB
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
In the given figure, seg XY || seg BC, then which of the following statements is true?

In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 10.8cm, BD = 4.5cm, AC = 4.8cm, and AE = 2.8cm
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
In any triangle _______ sides are opposite to equal angles
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
The ratio of the corresponding altitudes of two similar triangles is `3/5`. Is it correct to say that ratio of their areas is `6/5`? Why?
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

