Advertisements
Advertisements
Question
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
Options
ΔPQR ~ ΔCAB
ΔPQR ~ ΔABC
ΔCBA ~ ΔPQR
ΔBCA ~ ΔPQR
Solution
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ΔPQR ~ ΔCAB.
Explanation:
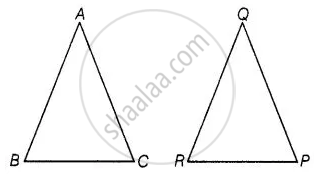
Given, in two ΔABC and ΔPQR,
`("AB")/("QR") = ("BC")/("PR") = ("CA")/("PQ")`
Which shows that sides of one triangle are proportional to the side of the other triangle, then their corresponding angles are also equal, so by SSS similarity, triangles are similar.
i.e., ΔCAB ∼ ΔPQR
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
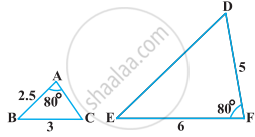
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
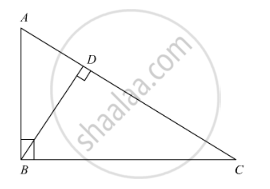
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In the following figure, AB || QR. Find the length of PB.

In the following Figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
State the AAA-similarity criterion
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
Which of the following is NOT a similarity criterion of traingles?
