Advertisements
Advertisements
Question
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution 1
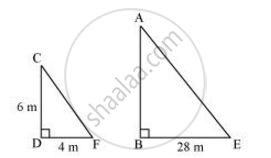
Let AB and CD be a tower and a pole respectively.
Let the shadow of BE and DF be the shadow of AB and CD respectively.
At the same time, the light rays from the sun will fall on the tower and the pole at the same angle.
Therefore, ∠DCF = ∠BAE
And, ∠DFC = ∠BEA
∠CDF = ∠ABE ...(Tower and pole are vertical to the ground)
∴ ΔABE ∼ ΔCDF ...(AAA similarity criterion)
⇒ `("AB")/("CB") = ("BE")/("DF")`
⇒ `("AB")/(6"m") = 28/4`
⇒ AB = 42 m
Therefore, the height of the tower will be 42 metres.
Solution 2
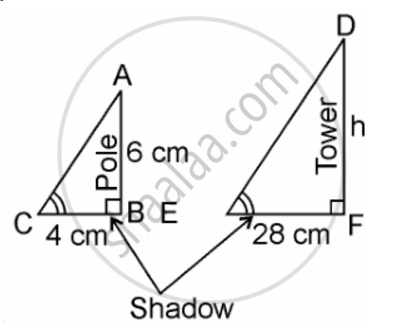
Length of the vertical pole = 6m ...(Given)
Shadow of the pole = 4 m ...(Given)
Let Height of tower = h m
Length of shadow of the tower = 28 m ...(Given)
In ΔABC and ΔDEF,
∠C = ∠E ...(angular elevation of sum)
∠B = ∠F = 90°
∴ ΔABC ~ ΔDEF ...(By AA similarity criterion)
∴ `"AB"/"DF" = "BC"/"EF"` ...(If two triangles are similar corresponding sides are proportional)
∴ `6/h = 4/28`
⇒ `h = (6×28)/4`
⇒ h = 6 × 7
⇒ h = 42 m
Hence, the height of the tower is 42 m.
APPEARS IN
RELATED QUESTIONS
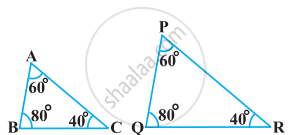
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
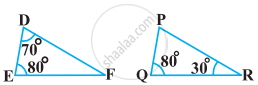
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
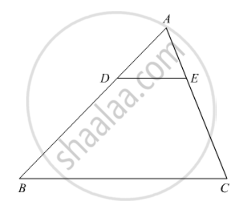
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In the given figure MN|| BC and AM: MB= 1: 2
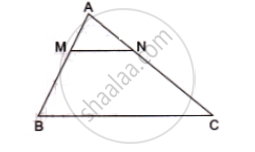
find ` (area(ΔAMN))/(area(ΔABC))`
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.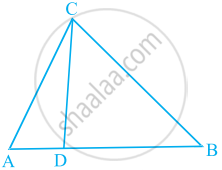
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
