Advertisements
Advertisements
Question
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
Options
47°
50°
83°
130°
Solution
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal 50°.
Explanation:
We have,
In triangle ABC and DEF,
RELATED QUESTIONS
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
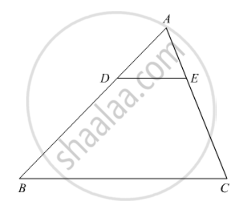
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii)
The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
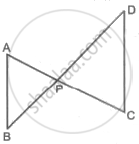
In the above figure, seg AC and seg BD intersect each other in point P. If
Activity: In ΔABP and ΔCDP
∴ ∠APB ≅
∴
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
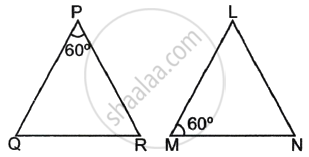
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅
⇒ ∠L =
We know, the sum of angles of a triangle =
∴ ∠L + ∠M + ∠N =
Substituting the values of ∠L and ∠M in equation (i),
∠N +
∠N =
∠N =
Hence, the measure of ∠N is
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
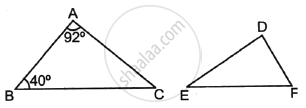
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
