Advertisements
Advertisements
Question
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
Solution 1
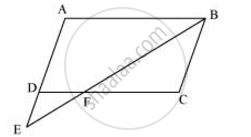
In ΔABE and ΔCFB,
∠BAE = ∠FCB ...(Opposite angles of a parallelogram)
∠AEB = ∠CBF ...(Alternate interior angles as AE || BC)
∴ ΔABE ∼ ΔCFB ...(By AA similarity criterion)
Solution 2
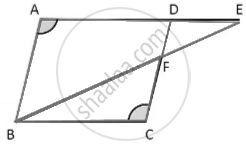
Given: A parallelogram ABCD where E is a point on side AD produced & BE intersects CD at F.
To Prove: ΔABE ~ ΔCFB.
Proof: In parallelogram ABCD,
opposite angles are equal,
Hence, ∠A = ∠C ...(1)
Also, In parallelogram ABCD opposite sides are parallel, AD || BC
Now since AE is AD extended,
AE || BC
and BE is the traversal
∴ ∠AEB = ∠CBF ...(Alternate Angles) ...(2)
Now in Δ ABE & Δ CFB
∠A = ∠C ...[From (1)]
∠AEB = ∠CBF ...[From (2)]
∴ ΔABE ~ ΔCFB ...(AA similarity criterion)
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
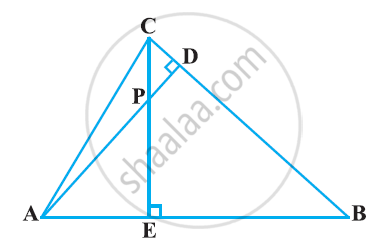
ΔAEP ∼ ΔADB
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?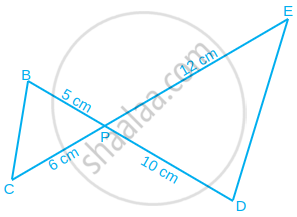
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?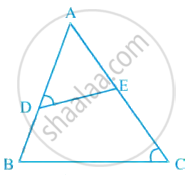
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
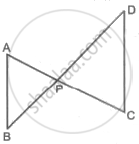
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
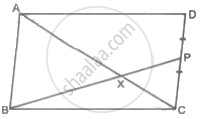
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
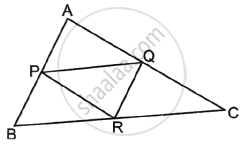
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

