Advertisements
Advertisements
प्रश्न
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
उत्तर

Let AB be A ladder and B is the window at 8 m above the ground C.
Now, In right triangle ABC
By using Pythagoras theorem, we have
`AB^2=BC^2+CA^2`
⇒ `10^2=8^2+CA^2`
⇒ `CA^2=100-64`
⇒ `CA^2=36`
⇒` CA=6m`
Hence, the distance of the foot of the ladder from the base of the wall is 6 m.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
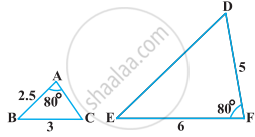
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
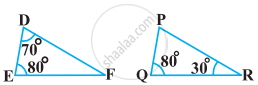
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
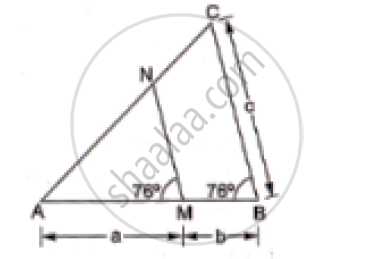
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

