English Medium
Academic Year: 2022-2023
Date: March 2023
Duration: 3h
Advertisements
General Instructions:
- This Question Paper has 5 Sections A-E.
- Section A has 20 MCQs carrying 1 mark each.
- Section B has 5 questions carrying 02 marks each.
- Section C has 6 questions carrying 03 marks each.
- Section D has 4 questions carrying 05 marks each.
- Section E has 3 case based integrated units of assessment (04 marks each) with sub-parts of the values of 1, 1, and 2 marks each respectively.
- All Questions are compulsory. However, an internal choice in 2 Questions of 5 marks, 2 Questions of 3 marks, and 2 Questions of 2 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take π =22/7 wherever required if not stated.
Let a and b be two positive integers such that a = p3q4 and b = p2q3, where p and q are prime numbers. If HCF (a, b) = pmqn and LCM (a, b) = prqs, then (m + n)(r + s) = ______.
15
30
35
72
Chapter: [0.011000000000000001] Real Numbers
Let p be a prime number. The quadratic equation having its roots as factors of p is ______.
x2 – px + p = 0
x2 – (p + 1)x + p = 0
x2 + (p + 1)x + p = 0
x2 – px + p + 1= 0
Chapter: [0.023] Quadratic Equations
If α and β are the zeros of a polynomial f(x) = px2 – 2x + 3p and α + β = αβ, then p is ______.
`(-2)/3`
`2/3`
`1/3`
`(-1)/3`
Chapter: [0.021] Polynomials
If the system of equations 3x + y = 1 and (2k – 1)x + (k – 1)y = 2k + 1 is inconsistent, then k = ______.
–1
0
1
2
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
If the vertices of a parallelogram PQRS taken in order are P(3, 4), Q(–2, 3) and R(–3, –2), then the coordinates of its fourth vertex S are ______.
(–2, – 1)
(–2, –3)
(2, –1)
(1, 2)
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
16 : 81
4 : 9
3 : 2
2 : 3
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
If x tan 60° cos 60°= sin 60° cot 60°, then x = ______.
cos 30°
tan 30°
sin 30°
cot 30°
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
If sin θ + cos θ = `sqrt(2)` then tan θ + cot θ = ______.
1
2
3
4
Chapter: [0.051] Introduction to Trigonometry
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
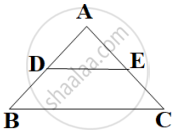
x = `(a + b)/(ay)`
y = `(ax)/(a + b)`
x = `(ay)/(a + b)`
`x/y = a/b`
Chapter: [0.040999999999999995] Triangles
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
6 cm
7 cm
8 cm
9 cm
Chapter: [0.040999999999999995] Triangles
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
`(3sqrt(3))/2 ` cm
6 cm
3 cm
`3sqrt(3)` cm
Chapter: [0.042] Circles
The area of the circle that can be inscribed in a square of side 6 cm is ______.
36π cm2
18π cm2
12π cm2
9π cm2
Chapter: [0.061] Areas Related to Circles
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
48 cm2
72 cm2
96 cm2
108 cm2
Chapter: [0.062] Surface Areas and Volumes
If the difference of Mode and Median of a data is 24, then the difference of median and mean is ______.
12
24
8
36
Chapter: [0.071] Statistics
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
2800
4000
5500
7000
Chapter: [0.061] Areas Related to Circles
For the following distribution:
| Class | 0 – 5 | 5 – 10 | 10 – 15 | 15 – 20 | 20 – 25 |
| Frequency | 10 | 15 | 12 | 20 | 9 |
The sum of lower limits of the median class and modal class is:
15
25
30
35
Chapter: [0.071] Statistics
Two dice are rolled simultaneously. What is the probability that 6 will come up at least once?
`1/6`
`7/36`
`11/36`
`13/36`
Chapter: [0.07200000000000001] Probability
Advertisements
If 5 tan β = 4, then `(5 sin β - 2 cos β)/(5 sin β + 2 cos β)` = ______.
`1/3`
`2/5`
`3/5`
6
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
Statement A (Assertion): If product of two numbers is 5780 and their HCF is 17, then their LCM is 340.
Statement R (Reason): HCF is always a factor of LCM.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
Chapter: [0.011000000000000001] Real Numbers
Statement A (Assertion): If the coordinates of the mid-points of the sides AB and AC of ∆ABC are D(3, 5) and E(–3, –3) respectively, then BC = 20 units.
Statement R (Reason): The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Assertion (A) is true but reason(R) is false.
Assertion (A) is false but reason(R) is true.
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
If 49x + 51y = 499, 51x + 49y = 501, then find the value of x and y.
Chapter:
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

Chapter: [0.040999999999999995] Triangles
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.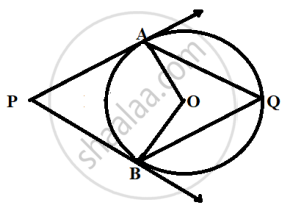
Chapter: [0.042] Circles
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
Chapter: [0.061] Areas Related to Circles
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
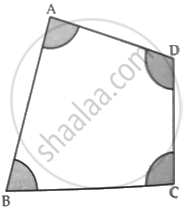
Chapter: [0.061] Areas Related to Circles
If sin(A + B) = 1 and cos(A – B)= `sqrt(3)/2`, 0° < A + B ≤ 90° and A > B, then find the measures of angles A and B.
Chapter: [0.051] Introduction to Trigonometry
Find an acute angle θ when `(cos θ - sin θ)/(cos θ + sin θ) = (1 - sqrt(3))/(1 + sqrt(3))`
Chapter: [0.051] Introduction to Trigonometry
Given that `sqrt(3)` is irrational, prove that `5 + 2sqrt(3)` is irrational.
Chapter: [0.011000000000000001] Real Numbers
If the zeroes of the polynomial x2 + px + q are double in value to the zeroes of the polynomial 2x2 – 5x – 3, then find the values of p and q.
Chapter: [0.021] Polynomials
A train covered a certain distance at a uniform speed. If the train would have been 6 km/h faster, it would have taken 4 hours less than the scheduled time. And, if the train was slower by 6 km/h it would have taken 6 hours more than the scheduled time. Find the length of the journey.
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
Anuj had some chocolates, and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 chocolates and the second lot at the rate of ₹ 1 per chocolate, and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per chocolate, and the second lot at the rate of ₹4 for 5 chocolates, his total collection would have been ₹460. Find the total number of chocolates he had.
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
Advertisements
Prove the following that:
`tan^3θ/(1 + tan^2θ) + cot^3θ/(1 + cot^2θ)` = secθ cosecθ – 2 sinθ cosθ
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
Prove that a parallelogram circumscribing a circle is a rhombus.
Chapter: [0.042] Circles
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°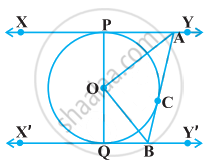
Chapter: [0.042] Circles
Two coins are tossed simultaneously. Find the probability of getting at least 1 head.
Chapter: [0.07200000000000001] Probability
Two coins are tossed simultaneously. What is the probability of getting at most one tail?
Chapter: [0.07200000000000001] Probability
Two coins are tossed simultaneously. What is the probability of getting a head and a tail?
Chapter: [0.07200000000000001] Probability
To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool?
Chapter: [0.023] Quadratic Equations
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed for the trip was reduced by 200 km/hr and the time of the flight increased by 30 minutes. Find the scheduled duration of the flight.
Chapter: [0.023] Quadratic Equations
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
Chapter: [0.062] Surface Areas and Volumes
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
Chapter: [0.062] Surface Areas and Volumes
The median of the following data is 525. Find the values of x and y, if the total frequency is 100.
| Class interval | Frequency |
| 0 – 100 | 2 |
| 100 – 200 | 5 |
| 200 – 300 | x |
| 300 – 400 | 12 |
| 400 – 500 | 17 |
| 500 – 600 | 20 |
| 600 – 700 | y |
| 700 – 800 | 9 |
| 800 – 900 | 7 |
| 900 – 1000 | 4 |
Chapter: [0.071] Statistics
A tiling or tessellation of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. Historically, tessellations were used in ancient Rome and in Islamic art. You may find tessellation patterns on floors, walls, paintings etc. Shown below is a tiled floor in the archaeological Museum of Seville, made using squares, triangles and hexagons.

A craftsman thought of making a floor pattern after being inspired by the above design. To ensure accuracy in his work, he made the pattern on the Cartesian plane. He used regular octagons, squares and triangles for his floor tessellation pattern
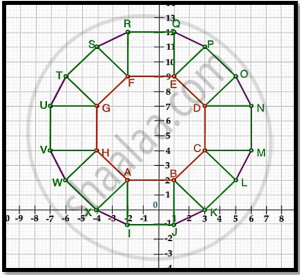
Use the above figure to answer the questions that follow:
- What is the length of the line segment joining points B and F?
- The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
- What are the coordinates of the point on y-axis equidistant from A and G?
OR
What is the area of Trapezium AFGH?
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
The school auditorium was to be constructed to accommodate at least 1500 people. The chairs are to be placed in concentric circular arrangement in such a way that each succeeding circular row has 10 seats more than the previous one.
- If the first circular row has 30 seats, how many seats will be there in the 10th row?
- For 1500 seats in the auditorium, how many rows need to be there?
OR
If 1500 seats are to be arranged in the auditorium, how many seats are still left to be put after the 10th row? - If there were 17 rows in the auditorium, how many seats will be there in the middle row?
Chapter: [0.024] Arithmetic Progressions
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
Chapter: [0.053] Some Applications of Trigonometry
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2022 - 2023
Previous year Question paper for CBSE Class 10 Maths-2023 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
