Question

We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.

At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-

1. Draw a neat labelled figure to show the above situation diagrammatically.
2. What is the distance travelled by the plane in 30 seconds?
   OR
   Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration.
3. What is the speed of the plane in km/hr.

Answer 1

i. 

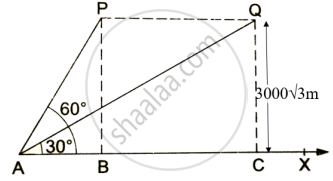
P and Q are the two positions of the plane flying at a height of `3000sqrt(3)` m. A is the point of observation.

ii. In ΔPAB, tan 60° = `(PB)/(AB)`

Or `sqrt(3) = (3000sqrt(3))/(AB)`

So AB = 3000 m

tan 30° = `(QC)/(AC)`

`1/sqrt(3) = (3000sqrt(3))/(AC)`

AC = 9000 m

Distance covered = 9000 – 3000

= 6000 m

OR

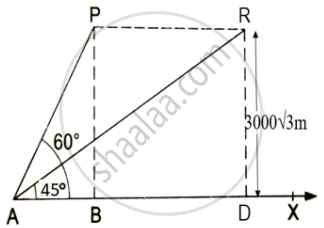
In ΔPAB, tan 60° = `(PB)/(AB)`

Or `sqrt(3) = (3000sqrt(3))/(AB)`

So AB = 3000 m

tan 45° = `(RD)/(AD)`

1 = `(3000sqrt(3))/(AD)`

AD = `3000sqrt(3)` m

Distance covered = `3000sqrt(3) - 3000`

= `3000(sqrt(3) -1)` m.

iii. Speed = `6000/30`

= 200 m/s

= `200 xx 3600/1000`

= 720 km/hr

Alternatively: speed = `(3000(sqrt(3) - 1))/(15(sqrt(3) - 1))`

= 200 m/s

= `200 xx 3600/1000`

= 720 km/hr