Advertisements
Advertisements
Question
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Solution
Let AB be the string of string x m. let DF be the ground and a boy flying the kite of 100 m string at an elevation of 30 °. And another boy flying the kite of 10 m high building at an angle of elevation of 45°.
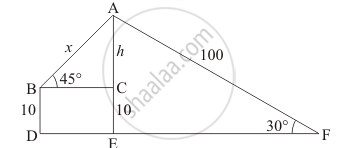
Let AE = H, AC = h, CE = 10, AB = x and AF = 100 m
∠ABC = 45°, ∠AFE = 30°
Here we have to find length of string.
We use trigonometric ratios.
`In ΔAFE`
`=> sin 30^@ = (AE)/(AF)`
`=> 1/2 = H/100`
=> h = 50
=> h = H - 10
=> h = 50 - 10
=> h = 40
Again in ΔABC
`=> sin 45^@ = (AB)/(AC)`
`=> 1/sqrt2 = h/x`
`=> 1/sqrt2 = 40/x`
`=> x = 40sqrt2`
Hence the leght of string is `40sqrt2`
APPEARS IN
RELATED QUESTIONS
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
