Advertisements
Advertisements
Question
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
Solution
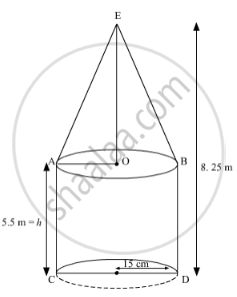
It is given that, radius of cylinder `(r_1)=30/2m=15m`
Height of cylinder (h1) = 5.5 m
And, height of the tent (H) = 8.25 m
So, height of cone (h2) = 8.25 m − 5.50 m = 2.75 m
And, radius of cone (r2) = 15 m
Let the slant height of the cone be l m.
`therefore l^2=(15m)^2+(2.75m)^2`
`rArr l^2=(225+7.5625)m^2`
`rArr l=sqrt232.5625m`
`rArrl=15.25 m`
Curved surface area of the tent = Curved surface area of cylinder + Curved surface area
of cone
`=2pir_1h_1+pir_2l`
`=(2xx22/7xx15xx5.5)cm^2+22/7xx15xx15.25cm^2`
`=(518.57+718.93)cm^2`
`=1237.5m^2`
Now, curved surface area of the tent is equal to the area of rectangular piece of canvas.
It is given that, breadth of canvas = 1.5 m
Let l be the length of canvas.
∴l × 1.5 = 1237.5
`rArrl=1237.5/1.5=825m`
Hence, the length of canvas used in making the tent is 825 m.
APPEARS IN
RELATED QUESTIONS
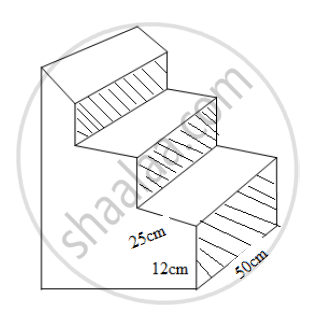
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
Find the distance between the points (a, b) and (−a, −b).
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
