Advertisements
Advertisements
Question
Find the distance between the points (a, b) and (−a, −b).
Solution
Using distance formula:
`d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
Here, x1 = a, y1 = b, x2 = -a and y2 = -b
On substituting the values in the formula we get
`sqrt((-a - a)^2 + (-b-b)^2)`
= `sqrt((-2a)^2 + (-2b)^2)`
=`sqrt(4a^2 + 4b^2)`
= `2sqrt(a^2 + b^2)`
Therefore, the distance between (a,b) and (-a,-b) is `2sqrt((a^2) + (b^2))`
APPEARS IN
RELATED QUESTIONS
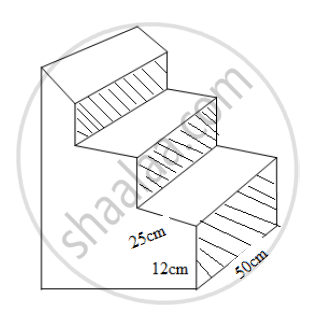
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
In given figure, the length of AP is ____________.

An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
