Advertisements
Advertisements
Question
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
Solution 1
Let AB be the tower and BC be the flagstaff.
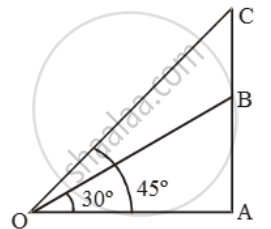
Then, BC = 7 m. Let AB = h.
Let O be the point of observation.
Then, ∠AOB = 30º and ∠AOC = 45º.
`\text{Now, }\frac{OA}{AC}=\text{cot 45}^\text{o}=1`
⇒ OA = AC = h + 7.
`\text{And, }\frac{OA}{AB}=\text{cot }30^\text{o}=\sqrt{3}`
`\Rightarrow \frac{OA}{h}=\sqrt{3}\Rightarrow OA=h\sqrt{3}`
∴ h + 7 = h√3
`\Rightarrow \frac{7}{\sqrt{3}-1}\times\frac{\sqrt{3}+1}{\sqrt{3}+1}=\frac{7(\sqrt{3}+1)}{2}=9.562\m`
Solution 2
Let BC be the tower of height hm. AB be the flagstaff of height 7 m on the tower and Dbe the point on the plane making an angle of elevation of the top of the flagstaff is 45° and angle of elevation of the bottom of the flagstaff is 30°.
Let CD = x, AB = 7 and ∠BDC = 30° and ∠ADC = 45°.
We to find the height of the tower
We have the corresponding figure as follows
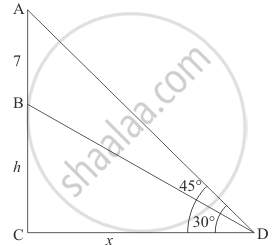
So we use trigonometric ratios.
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 30^@ = h/x`
`=> 1/sqrt3 = h/x`
`=> x = sqrt3h`
Again in a triangle ADC
`=> tan D = (AB + BC)/(CD)`
`=> tan 45^@ = (h + 7)/x`
`=> 1 = (h + 7)/x`
`=> x = h + 7`
`=> sqrt3h = h + 7`
`=> h(sqrt3 - 1) = 7`
`=> h = 7/(sqrt3 - 1)`
`=> h = 9.56`
Hence the height of toweris 9.56 m
APPEARS IN
RELATED QUESTIONS
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
The line drawn from the eye of an observer to the point in the object viewed by the observer is known as ____________.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
