Advertisements
Advertisements
Question
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
Solution
Let AB be the tree of height h. And the top of the tree makes an angle of 30° with the ground. The distance between the foot of the tree to the point where the top touches the ground is 10 M.
lET bc = 10 And ∠ACB = 30°
Here we have to find the height of the tree.
Here we have the corresponding figure
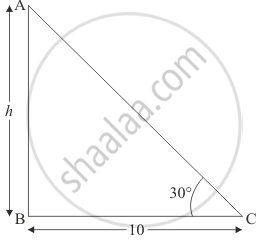
So we use trigonometric ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = (AB)/((BC)`
`=> 1/sqrt3 = h/10`
`=> h = 10/sqrt3`
Now in triangle ABC we have
`sin 30^@ = h/(AC)`
`=> 1/2 = 10/(sqrt3 AC)`
`=> AC = 20/sqrt3`
So the length of the tree is
` = AB + AC`
= h + AC
`= 10/sqrt3 + 20/sqrt3`
`= 10sqrt3`
= 1.73
Hence the height of tree is 17.3 m
APPEARS IN
RELATED QUESTIONS
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.

