Advertisements
Advertisements
प्रश्न
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
उत्तर
Let AB be the tree of height h. And the top of the tree makes an angle of 30° with the ground. The distance between the foot of the tree to the point where the top touches the ground is 10 M.
lET bc = 10 And ∠ACB = 30°
Here we have to find the height of the tree.
Here we have the corresponding figure
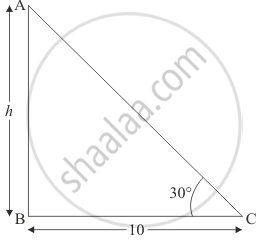
So we use trigonometric ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = (AB)/((BC)`
`=> 1/sqrt3 = h/10`
`=> h = 10/sqrt3`
Now in triangle ABC we have
`sin 30^@ = h/(AC)`
`=> 1/2 = 10/(sqrt3 AC)`
`=> AC = 20/sqrt3`
So the length of the tree is
` = AB + AC`
= h + AC
`= 10/sqrt3 + 20/sqrt3`
`= 10sqrt3`
= 1.73
Hence the height of tree is 17.3 m
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
