Advertisements
Advertisements
प्रश्न
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
उत्तर १
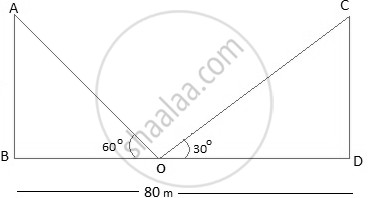
Let AB and CD be the poles and O is the point from where the elevation angles are measured.
In ΔABO
`("AB")/("BO") = tan 60°`
`("AB")/("BO") = sqrt3`
`"BO" = ("AB")/sqrt3`
In ΔCDO,
`("CD")/("DO") = tan 30°`
`("CD")/(80-"BO") = 1/sqrt3`
`"CD"sqrt3 = 80 - "BO"`
`"CD"sqrt3 = 80 - ("AB")/sqrt3`
`"CD"sqrt3+ ("AB")/sqrt3 = 80`
Since the poles are of equal heights,
CD = AB
`"CD"[sqrt3 + 1/sqrt3] = 80`
`"CD"((3+1)/sqrt3) = 80`
`"CD" = 20sqrt3`
`"BO"= ("AB")/sqrt3 = ("CD")/sqrt3`
= `((20sqrt3)/sqrt3)`m
= 20 m
DO = BD − BO
= (80 − 20) m
= 60 m
Therefore, the height of poles is `20sqrt3` and the point is 20 m and 60 m far from these poles.
उत्तर २
Let AB and CD be the two poles of equal height.
O be the point makes an angle of elevation from the top of the poles of 60° and 30°, respectively.
Let OA = 80 - x, OD = x.
And ∠BOA = 30°, ∠COD = 60°.
Here, we have to find the height of the poles and the distance of the points from the poles.
We have the corresponding figure as follows:.
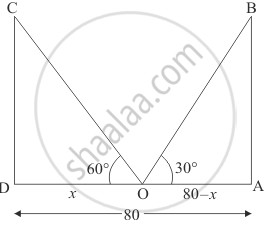
So we use trigonometric ratios.
In a triangle COD,
⇒ tan 60° = `"CD"/"DO"`
⇒ `sqrt(3) = "h"/"x"`
⇒ `"x" = "h"/sqrt(3)`
Again in a triangle AOB,
⇒ tan 30° = `"AB"/"OA"`
⇒ `(1)/sqrt(3) = "h"/(80 -"x")`
⇒ `sqrt(3)"h" = 80 - "x"`
⇒ `sqrt(3)"h" = 80 - "h"/sqrt(3)`
⇒ `sqrt(3)"h" + "h"/sqrt(3) = 80`
⇒ `3"h" + "h" = 80sqrt(3)`
⇒ `4"h" = 80sqrt(3)`
⇒ `"h" = 20sqrt(3)`
⇒ `"x" = (20sqrt(3))/sqrt(3)`
⇒ x = 20
And
⇒ OA = 80 - x
⇒ OA = 80 - 20
⇒ OA = 60
Hence, the height of pole is `20sqrt(3)` and distances are 20m, 60m respectively.
APPEARS IN
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
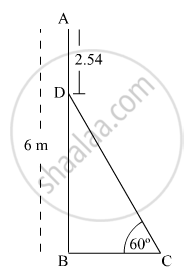
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
