Advertisements
Advertisements
प्रश्न
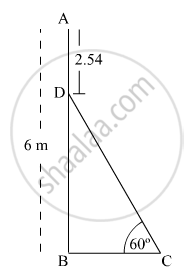
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
उत्तर
In the given figure,
AB = AD + DB = 6 m
Given: AD = 2.54 m
⇒ 2.54 m + DB = 6 m
⇒ DB = 3.46 m
Now, in the right triangle BCD,
`(BD)/(CD)=sin 60^@`
`=>(3.46m)/(CD)=sqrt3/2`
`=>(3.46m)/(CD)=1.73/2`
`=>CD=(2xx3.46m)/1.73`
⇒CD=4 m
Thus, the length of the ladder CD is 4 m.
APPEARS IN
संबंधित प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
