Advertisements
Advertisements
प्रश्न
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
उत्तर
Let AB be the tower of height h and AD be the flagpole on the tower. At the point 9m away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole is 60° and 30°
Let AD = x, BC = 9 and ∠ACB = 30°, ∠DCB = 60°
Here we have to find the height of tower and height of the flagpole.
The corresponding diagram is as follows
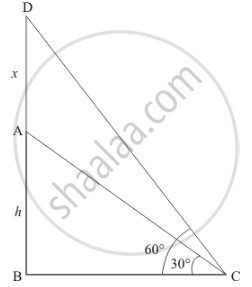
In a triangle ABC,
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = h/9`
`=> 1/sqrt3 = h/9`
`=>h = 9/sqrt3`
`=> h = 3sqrt3`
Again in a triangle DBC
`=> tan C = (AD + AB)/(BC)`
`=> tan 60^@ = (h + x)/9`
`=> sqrt3 = (h + x)/9`
`=> 9sqrt3 = h + x`
`=> 9sqrt3 = 3sqrt3 + x`
`=> x = 6sqrt3`
So height of tower is `3sqrt3` meter and height of flag pole is `6sqrt3` meters
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
