Advertisements
Advertisements
प्रश्न
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
उत्तर
Let the observer be at point C on the ground.
∴ ∠C = 30°
He moves 20 m towards the tower and reaches point D.
∴ ∠D = 30° + 15° = 45°
Let the distance BD be x m and the height of the tower be h m.
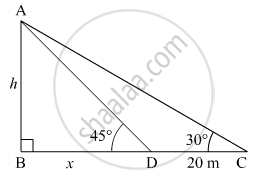
In ΔABD
`tan 45^@ = "AB"/"BD" = h/x`
`=> 1 = h/x`
`=> h = x`
In ΔABC
`tan 30^@ = (AB)/(BC) = h/(x + 20) = h/(h + 20)`
`=> 1/sqrt3 = h/(h + 20)`
`=> h + 20 = sqrt3h`
`=> h = 20/(sqrt3 - 1) =10(sqrt3 + 1) m`
Hence, the height of the tower is `10(sqrt3+1)` m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
The Distance of the point (−3, 4) from the x-axis is
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
