Advertisements
Advertisements
प्रश्न
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
उत्तर
Let the observer be at point C on the ground.
∴ ∠C = 30°
He moves 20 m towards the tower and reaches point D.
∴ ∠D = 30° + 15° = 45°
Let the distance BD be x m and the height of the tower be h m.
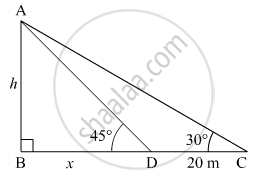
In ΔABD
`tan 45^@ = "AB"/"BD" = h/x`
`=> 1 = h/x`
`=> h = x`
In ΔABC
`tan 30^@ = (AB)/(BC) = h/(x + 20) = h/(h + 20)`
`=> 1/sqrt3 = h/(h + 20)`
`=> h + 20 = sqrt3h`
`=> h = 20/(sqrt3 - 1) =10(sqrt3 + 1) m`
Hence, the height of the tower is `10(sqrt3+1)` m
APPEARS IN
संबंधित प्रश्न
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
