Advertisements
Advertisements
प्रश्न
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
उत्तर
Let AB be the height of tower 50 m and angle of depression from the top of the tower are 60° and 30° respectively at two observing Car C and D.
Let BD = x m, CD = y m and ∠ADB = 30°, ∠ACb = 60°
We have the corresponding figure as follows
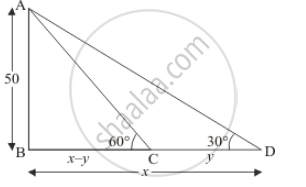
So we use trigonometric ratios.
In a triangle ABD
`=> tan D = (AB)/(BD)`
`=> tan 30° = 50/x`
`=> 1/sqrt3 = 50/x`
`=> x = 50sqrt3`
Since x = 86.6
Again in a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60° = 50/(x - y)`
`=> sqrt3 = 50/(x - y)`
`=> sqrtt3 xx 50sqrt3 - sqrt3y = 50`
`=> y = 57.67`
Therefore x - y= 86.6 - 57.67
`=> x - y = 28.93`
Hence the distance of first car from tower is 86.6 m
And the distance of second car from tower is 57.67 m
And the distance between cars is 28.93 m
APPEARS IN
संबंधित प्रश्न
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is
`\frac{h(\tan\alpha +\tan \beta )}{\tan \beta -\tan \alpha }`
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
