Advertisements
Advertisements
प्रश्न
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
उत्तर
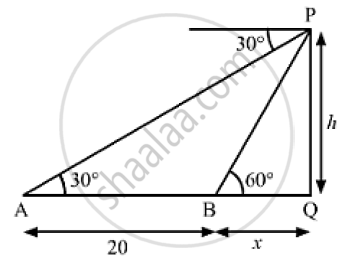
Let PQ be the tower.
We have,
AB = 20m, ∠PAQ = 30° and ∠PBQ = 60°
Let BQ = x and PQ = h
In ΔPBQ,
` tan 60° = (PQ)/(BQ) `
`⇒ sqrt(3) = h/x`
`⇒ = x sqrt(3) ` .......(1)
Also, in ΔAPQ ,
` tan 30° = (PQ)/(AQ)`
`⇒ 1/ sqrt(3) = h/(AB +BQ)`
`⇒ 1/ sqrt(3) = (x sqrt(3))/(20+x)` [Using (1)]
⇒ 20+ x = 3x
⇒ 3x -x = 20
⇒ 2x = 20
`⇒ =20/2`
⇒ x = 10 m
From (i),
`h = 10 sqrt(3)=10xx1.732 =17.32m`
Also, AQ = AB+BQ = 20 + 10 = 30m
So, the height of the tower is 17. 32 m and its distance from the point A is 30 m.
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
